Grundlagen: Dämpfungsglied

zurück zu HF , zurück zur Elektronik , Homepage

Einleitung

PI-Schaltung
T-Schaltung

Einleitung

Ein Dämpfungsglied (Attenuator) soll nur einen bestimmten Teil der eingespeisten Leistung an Ausgang herauslassen. Die restliche Energie soll nicht weiter stören, also muss sie "vernichtet" werden. Das geht gut durch einen Widerstand, der überschüssige Leistung in Wärme umwandelt.

Außerdem, müssen wir die Impedanz beachten. Ein Dämpfungsglied soll dann gut funktionieren, wenn am Ausgang etwas mit der korrekten Impedanz von 50 Ohm angeschlossen ist. Außerdem muss dann das Dämpfungsglied selber am Eingang eine Impedanz von 50 Ohm aufweisen.

Ein Dämpfungsglied enthält normalerweise drei Widerstände, die entweder in PI-Schaltung oder in T-Schaltung angeordnet sind.

PI-Schaltung
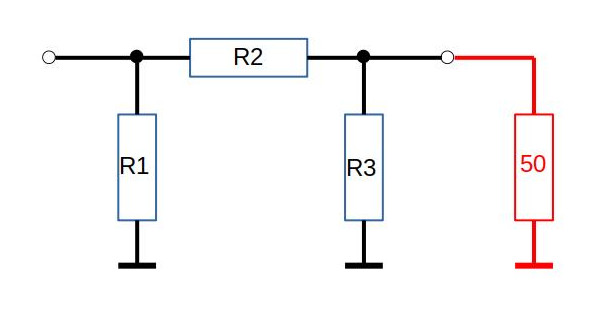
Diese Grafik zeigt die PI-Schaltung. Zusätzlich ist in rot die am Ausgang angeschlossene Schaltung (mit 50 Ohm Impedanz) dargestellt. Da ein Dämpfungsglied normalerweise in beide Richtungen gleich funktionieren soll, ist es symmetrisch aufgebaut. Das bedeutet, dass die Widerstände R1 und R3 identisch sind.

Elektroniker haben mit Widerständen kein Problem. In dieser Schaltung sehen wir einen Spannungsteiler bestehend aus R2 und der Parallelschaltung aus R3 und den externen 50-Ohm. Der Spannungsteiler sorgt dafür, dass die Ausgangsspannung genau ein bestimmter Teil der Eingangsspannung ist, und das Spannungsteilverhältnis (Vu) lässt sich auch leicht ausrechnen:

Vu = (R3||50) / (R2 + (R3||50))

wobei "||" für die Parallelschaltung zweier Widerstände steht.

Die Leistung steht in quadratischer Beziehung zur Spannung. Halbe Spannung bedeutet zum Beispiel ein Viertel der Leistung. Das liegt daran, dass sich bei halber Spannung ja auch der Strom durch einen konstanten Widerstand halbiert, und die Leistung das Produkt aus Spannung und Strom ist: 1/2 x 1/2 = 1/4

Beispiel:
Ein 5dB Dämpfungsglied, soll die Leistung um 5 dB verringern. Dann muss die Ausgangsleistung das 0,316-fache der Eingangsleistung (10^(-5/10) = 0,316) betragen. Für das Spannungsverhältnis müssen wir daraus die Wurzel berechnen (um das quadratische Verhältnis wieder zu kompensieren). Das ergibt eine Ausgangsspannung vom 0,5623-fachen der Eingangsspannung. Die obige Formel für Vu muss also Vu = 0,5623 ergeben. (Man kann auch gleich 10^(-5/20) = 0,5623 rechnen.)

Es lässt sich nun aber für jeden beliebigen R3-Wert ein passender R2-Wert bestimmen, mit dem die Formel den gewünschten Wert ergibt.

Leider gibt es aber noch eine zweite wichtige Bedingung. Die gesamte abgebildete Schaltung muss ja auch 50 Ohm Impedanz (also Eingangswiderstand) haben. Es gilt also auch:

R1 || (R2 + (R3||50)) = 50

und da R1 und R3 aus Symmetriegründen gleich sein sollen, folgt:

R3 || (R2 + (R3||50)) = 50

Ok. Damit bleibt genau noch eine Kombination von R2 und R3 (=R1) übrig, die beide Formeln erfüllt. Für die üblichen Dämpfungen habe ich die Werte (in Ohm) hier mal aufgelistet:

Dämpfung	R1=R3	R2
1 dB	896,5	5,77
2 dB	436,2	11,6
5 dB	178,5	30,4
10 dB	96,25	71,15
20 dB	61,11	247,5
30 dB	53,27	789,8

Das sind nicht gerade die üblichen Widerstands-Werte aus den E-Reihen, die man im Bastlerladen kaufen kann, aber man sollte sich ihnen so dicht wie möglich annähern.

Die Suchmaschine des Vertrauens wird bei "pi attenuator power calculator" einige Online-Tools für die Berechnung finden, bei denen man auch eigene (angenäherte) Widerstandswerte eingeben kann. Sie berechnet dann die damit festgelegte Dämpfung in dB und den am Eingang wegen falscher Impedanz zurückreflektierten Teil der eingespeisten Leistung (return loss). Mir gefällt: https://leleivre.com/rf_pipad.html

Will man sein eigenes DIY-Dämpfungsglied bauen, sollte man auf SMD-Widerstände zurückgreifen, da diese bei höheren Frequenzen (im Vergleich zu bedrahteten Widerständen) weniger störende Induktivität aufweisen.

T-Schaltung
Diese Grafik zeigt die T-Schaltung. Zusätzlich ist in rot die am Ausgang angeschlossene Schaltung (mit 50 Ohm Impedanz) dargestellt. Da ein Dämpfungsglied normalerweise in beide Richtungen gleich funktionieren soll, ist es symmetrisch aufgebaut. Das bedeutet, dass die Widerstände R1 und R3 identisch sind.

Die Spannungsteilverhältnis Vk der Spannung am Knotenpunkt zwischen R1, R2 und R3 und der Eingangsspannung lässt sich wie folgt bestimmen:

Vk = ((R3 + 50) || R2) / (R1 + ((R3 + 50) || R2) )

Die Ausgangsspannung ist ein Teil dieser "Knotenpunktspannung". Die Größe dieses Teils hängt vom Verhältnis von R3 und Ausgangsimpedanz ab. Das ergibt dann für die Ausgangsspannung Vu:

Vu = Vk * 50 / (R3 + 50)

Vu = ((R3 + 50) || R2) / (R1 + ((R3 + 50) || R2) ) * 50 / (R3 + 50)

Vu = ((R3 + 50) || R2) / (R3 + ((R3 + 50) || R2) ) * 50 / (R3 + 50)

Wie schon beim PI-Attenuator lässt sich nun für jeden beliebigen R3-Wert ein passender R2-Wert bestimmen, mit dem die Formel den gewünschten Wert ergibt.

Die gesamte abgebildete Schaltung muss ja auch 50 Ohm Impedanz (also Eingangswiderstand) haben. Es gilt also auch:

R1 + (R2 || (R3 + 50)) = 50

und da R1 und R3 aus Symmetriegründen gleich sein sollen, folgt:

R3 + (R2 || (R3 + 50)) = 50

Für die üblichen Dämpfungen habe ich die sich ergebenden Werte (in Ohm) hier mal aufgelistet:

Dämpfung	R1=R3	R2
1 dB	2,9	433
2 dB	5,73	215
5 dB	14	82
10 dB	26	35
20 dB	41	10
30 dB	47	3,17

zurück zu HF , zurück zur Elektronik , Homepage

Autor: sprut
erstellt: 16.02.2019