Zur Anzeige wird der 10 bittig gemessene ADC-Wert 4-stellig am LCD dezimal angezeigt (in Millivolt).
Zum Aufbau eignet sich z.B. die 16F876-Testplatine.und die LCD-Adapterplatine.
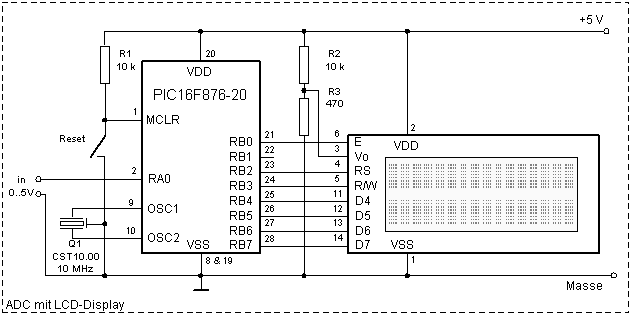
Beim Brennen des PIC ist der HS-Oszillator auszuwählen
Schaltung
Problem Nr. 1: Umrechnung in Millivolt
Problem Nr. 2: Umwandlung in eine Dezimalzahl
16-Bit Addition/Subtraktion
Division durch 2
Lösung für Problem Nr. 1: Umrechnung in
Millivolt
Lösung für Problem Nr. 2: Umwandlung einer
16 Bit Binärzahl in eine Dezimalzahl
eine analogen Eingangsspannung von 0V ... 5V wird gemessen und am
LCD angezeigt
Die Spannungsmessung und die binäre
Anzeige wurde schon behandelt.
Die Ansteuerung eines LCD ist auch nicht neu.
Will man aber die gemessene Spannung in Volt oder Millivolt am LCD
anzeigen, ist etwas 'Datenverarbeitung' nötig.
 |
Die Schaltung besteht lediglich aus einem PIC16F876 (oder
anderer 16F87x),
einer 10-MHz Schwinger und einem Dot-Matrix
Display. Die analoge Spannung wird an RA0 ind den PIC
gespeist.
Zur Anzeige wird der 10 bittig gemessene ADC-Wert 4-stellig am LCD dezimal angezeigt (in Millivolt). Zum Aufbau eignet sich z.B. die 16F876-Testplatine.und die LCD-Adapterplatine. Beim Brennen des PIC ist der HS-Oszillator auszuwählen |
Problem Nr. 1
Wird Vdd (+5V) als Referenzspannung verwendet, dann misst der
ADC mit einer Auflösung von 5V / 1024 = 4,8828125 mV.
Das binäre 10-Bit-Ergebnis der AD-Wandlung (Uadc) kann
in einen Millivoltwert umgewandelt werden, wenn es mit 4,8828125
multipliziert
wird.
U[mV] = 4,8828125 * UadcDas entspricht einer Multiplikation mit 5 und einer nachfolgenden Division durch 1,024.
In einem PIC lassen sich folgende Berechnungen leicht durchführen:
Die oben geforderte Multiplikation mit 5 lässt sich auf 2 Wegen einfach realisieren.
Die Division durch 1,024 ist etwas schwieriger. Es gilt aber
X / 1,024 = X - X/64 - X/128Damit ergibt sich also für die Spannung in Millivolt folgende Berechnungsmöglichkeit:
U[mV] = 5Uadc - 5Uadc/64 - 5Uadc/128Diese Berechnung lässt sich einfach auf Bitverschiebebefehle, eine 16-Bit-Addition und zwei 16-Bit Subtraktionen zurückführen. Auf richtige Multiplikationen und Divisionen lässt sich verzichten.
Problem Nr. 2
Wir haben nun die am Pin RA0 anliegende Spannung in Millivolt
ermittelt.
Unsere Zahl ist aber immer noch eine Binärzahl. Auf dem
LCD-Display
wollen wir aber eine Dezimalzahl anzeigen. Dazu ist eine
Binär-zu-Dezimal-Wandlung
nötig.
Zur Wandlung einer Binärzahl in eine Dezimalzahl gibt es
prinzipiell
zwei Möglichkeiten
Weg zur Lösung: 16-Bit
Addition/Subtraktion
Was wir unter allen Umständen benötigen ist die 16-Bit
Addition
und die 16-Bit Subtraktion. Beide benötigen jeweils ein kleines
Unterprogramm.
Da alle Register des PIC nur 8 Bit groß sind, lege ich je zwei
Register
fest, die jeweils zusammen eine 16-Bit Zahl speichern sollen:
16 Bit Addition
Nachfolgender Code zeigt eine 16-Bit Addition der Werte f (f1,f0) und
xw (xw1,xw0). Das 16-Bit Ergebnis wird in f gespeichert, xw wird nicht
verändert. Sollte das Ergebins 17 Bit groß sein, so wird zum
Zeichen des Überlaufs das C-Bit im Register STATUS gesetzt..
| ;*********************************************************************
;16 bit Adition, C-Flag bei Überlauf gesetzt Add16 ; 16-bit add: f := f + xw movf xw0,W ; xw0 nach W addwf f0,F ; f0 := f0 + xw0
movf
xw1,W
;
xw1 nach W return ; fertig |
16 Bit Subtraktion
Für die Subtraktion benötigen wir ein zusätzliches
Hilfsregister
'Fehler', in dem wir uns merken müssen, ob während der
Berechnung
ein Borgen von der höchsten Stelle nicht mehr möglich war,
also
ein Überlauf während der Berechnung auftrat. Auch muss des
C-Flag zum Schluss invertiert werden, da der SUBWF-Befehl genau beim
Überlauf kein C-setzt.
| ;*****************************************************
; 16 Bit Subtraktion, bei Überlauf (neg. Ergebnis) ist C gesetzt Sub16 ; 16 bit f:=f-xw clrf Fehler ; extraflags löschen
movf
xw0,
w
; f0:=f0-xw0
btfsc
STATUS,C
btfss
STATUS,C Sub16a
btfss
STATUS,C
bcf
STATUS, C ; C-Flag invertieren
|
Division durch 2
Dezimalzahlen (Zahlenbasis 10) kann man durch 10 dividieren, indem
man einfach alle Stellen der Dezimalzahl um eine Stelle nach rechts
verschiebt.
(1250 / 10 = 125)
Genauso kann man Binärzahlen (Zahlenbasis 2) durch 2 dividieren,
indem man alle Stellen der Binärzahl um einen Stelle nach rechs
verschiebt.
(101010b / 10b = 10101b)
Das erledigt für 8-Bit Zahlen der Verschiebebefehl RRF. Der
lässt
sich problemlos auf größere Zahlen anwenden, die über
mehrere
Register verteilt sind (z.B. xw1 und xw0).
Da wir Divisionen durch 64 und 128 benötigen, müssen wir
die
Division durch 2 also gleich mehrfach hintereinander anwenden. (64 =
2^6,
128 = 2^7) Das erledigt folgende Routine:
| ;*****************************************************
; Division durch 2 wird w-mal ausgeführt ; die zu dividierende Zahl steht in xw Div2 movwf counter ; Anzahl der Divisionen speichern Div2a ; 16 bit xw:=xw/2 bcf STATUS, C ; carry löschen rrf xw1, f rrf xw0, f
decfsz
counter
;
fertig? |
Lösung für Problem Nr. 1: Umrechnung
in
Millivolt
Damit haben wir nun alle nötigen Funktionen, um den ADC-Wert in
einen Millivolt-Wert unmzurechnen, entsprechend der Formel:
U[mV] = 5Uadc - 5Uadc/64 - 5Uadc/128
| ;*****************************************************
; Wandlung des ADC-Wert in Millivolt (binär) ; Der ADC-Wert steht in f1,f0 mV ; zunächst die Multiplikation mal 5 movfw f0 movwf xw0 movfw f1 movwf xw1 call Add16 ; f := 2xADC call Add16 ; f := 3xADC call Add16 ; f := 4xADC call Add16 ; f := 5xADC
;
ADC
* 5 nach xw kopieren
;
xw
durch 64 dividieren (6 mal durch 2) call Sub16 ; f := 5xADC - 5xADC/64
;
xw
auf 5xADC/128 verringern
call
Sub16
;
f := 5xADC - 5xADC/64 - 5xADC/128 |
Das hat doch gar nicht weh getan. Ganz ohne Fließkommaoperationen und ohne richtige Multiplikation/Division kommt man gelegentlich auch zum Ziel.
Lösung für Problem Nr. 2: Umwandlung
einer
16 Bit Binärzahl in eine Dezimalzahl
Das Messergebnis des ADC kann nach der Wandlung in Millivolt nicht
größer als ca. 5000 sein, da die maximale Eingangsspannung
5V
= 5000 mV beträgt.
Wenn man davon ausgeht, das der Wert mit Sicherheit unter 10000 liegt,
dann kann man wie folgt vorgehen.
Die Tausenderstelle des dezimalen Ergbnisses ermittelt man, indem
man
so oft es geht vom Millivoltwert 1000 abzieht.
Vom Rest zieht man so oft es geht 100 ab. Die Anzahl ergibt die
Hunderterstelle.
Dann zieht man vom verbleibenden Rest 10 ab, so oft es geht. Die Anzahl
ergibt die Zehnererstelle.
Der dann verbleibende Rest ist die Einerstelle.
Der nachfolgende Code enthält die komplette Wandlung. Das
Ergebnis
wird in 4 Registern (ST, SH, SZ, SE) dezimalstellenweise abgelegt.
| ;*****************************************************
; Wandlung einer Binärzahl (< 10000) in eine Dezimalzahl ; Die Binärzahl steht in f1,f0 ; die Dezimalstellen werden in ST (tausender), SH (hunderter), ; SZ (zehner) und SE (einer) gespeichert im BCD-Code B2D ; Test auf tausender 1000d = 0x03E8 movlw 0x03 movwf xw1 movlw 0xE8 movwf xw0 call B2Da movwf ST ; Test auf hunderter 100d = 0x0064 clrf xw1 movlw 0x64 movwf xw0 call B2Da movwf SH ; Test auf zehner 10d = 0x000A clrf xw1 movlw 0x0A movwf xw0 call B2Da movwf SZ movfw f0 movwf SE return B2Da |
Eigentlich können 16-Bit Zahlen größer als 9999 werden. Deshalb wäre eine Erweiterung um Zehntausender angebracht. Für unser ADC-Beispiel ist das aber nicht nötig.
Programmablauf
Programmlisting