Berechnung des Elektroantriebs

Einleitung
Motorleistung
Wie groß muss der Akku sein?
Was für einen Motorsteller braucht man?
Die Wahl des Motors
Die Luftschraube
Zusammenfassung
Datensammlungen , Software

Einleitung

Ganz anders geht die Antriebsdimensionierung im Elektroflug vor sich. Ein schwerer Akku speichert weniger als 1% der Energie, die in einem gleich schweren Benzintank enthalten ist. Hier wird um jedes Gramm Gewicht und um jedes Prozent Wirkungsgrad gekämpft. Von Leistungsüberschuss habe ich Elektroflieger noch nie reden hören. Um ein ansprechendes Flugzeug zu erhalten, ist eine genaue Abstimmung von Flugzeug, Akku, Motorsteller, Motor und Luftschraube nötig.

Die Wahl eines geeigneten Antriebs für ein Flugmodell ist nicht ganz einfach. Viele Motorhersteller bieten dem Modellbauer an, für sein Modell eine geeignetes Antriebsset (Motor + Motorsteller + Akku) zu ermitteln. Dabei kommt dann natürlich ein Set des Herstellers heraus. Ein paar grundlegende Gedanken kann sich aber zu diesem Problem jeder selber machen.
 

Motorleistung P

• 10 W/kg um einen Dauersegler etwas länger am Himmel zu halten
• 100 W/kg um in der Luft herumzuhungern
• 150 W/kg um normal fliegen zu können
• 200 W/kg für schnelles und manöverreiches Fliegen
• >200 W/kg für Kunstflug

Wie groß muss der Akku sein?

Ein 1,5 kg schweres Modell soll mit 150 W/kg motorisiert werden. Daraus lässt sich die nötige Motorleistung errechnen, die üblicherweise nicht in Pferdestärken sondern in Watt (W) angegeben wird.
Beispiel:
Gewicht : 1,5 kg
gewünschtes Leistungsgewicht: 150 W/kg
nötige elektrische Leistung: P = 1,5 kg x 150 W/kg = 225 W Motorleistung

Solange der Motor läuft verbraucht er Treibstoff, in unserem Fall elektrische Energie aus dem Akku. Die für eine bestimmte Motorlaufzeit nötige Energie ist das Produkt aus der Motorleistung und der Motorlaufzeit (Vollgas).
Beispiel:
Vollastmotorlaufzeit: 3 Minuten = 0,05 Stunden
Akkuenergie: E = 225 W x 0,05 h = 11,25 Wh

Damit steht fest, wieviel Energie ein Akku speichern muss, wenn er für 3 Minuten einen 225 W verbrauchenden Motor antreiben soll. Akkus werden aber nicht nach Energie E sondern nach Spannung U und Kapazität Q verkauft.

Akkukapazität Q
Um beim Vergleich von Akkuenergie und Benzin zu bleiben: Benzin kann je nach Volumen unterschiedlich viel Energie enthalten. SuperPlus enthält bei gleichem Volumen mehr Energie als Normalbenzin. Beim Akku entspricht sozusagen der Brennwert der Akkuspannung U  und das Volumen der Akkukapazität Q.

Jeder Akku besteht aus einzelnen Zellen, die je eine Spannung von ca 1,2 Volt (V) liefern. Soll ein 7-Zellen-Akku benutzt werden, so hat dieser eine Spannung von etwa
U =  7 x 1,2 V = 8,4 V.
Aus dem Fluggewicht und der erwünschten Flugleistung haben wir schon die nötige Akkuenergie E bestimmt. Für eine bestimmte Akkuspannung kann man nun die nötige Akkukapazität Q ausrechnen.

Akkukapazität = Akkuenergie / Akkuspannung = E / U = 11,25 Wh / 8,4 V = 1,34 Ah = 1340 mAh.

Ein 7-Zellen-Akku mit einer Kapazität von 1400 mAh wäre also geeignet.
Weiter unten kann man sehen, das in diesem Beispiel die Akkus mit einem Strom von 30 A belastet werden. Das verlangt gute Hochstromzellen (z.B. Sanyo).

---

Was für einen Motorsteller braucht man?

Beispiel:
elektrische Leistung P = 225 W
Akkuspannung: U = 8,4 V

I = P / U = 225 W /  8,4 V = 27 A

Falls der Akku bei diesem Strom auf 7,7 V zusammenbricht (1,1V pro Zelle) steigt der zu entnehmende Strom sogar auf 29 A. Der Motorsteller sollte also 3 Minuten lang einen Strom von 30 A verkraften können.
Da das Modell recht leicht ist, kann man vielleicht auf einen zusätzlichen Empfängerakku verzichten, wenn der Motorsteller einen BEC-Ausgang hat. Da man bei 3 Minuten Motorlaufzeit zwischendurch noch segeln wird, empfiehlt sich eine Klappluftschraube. Die verlangt nach einem Motorsteller mit Bremse.

---

Die Wahl des Motors

Leerlaufdrehzahl nleer
Die Leerlaufdrehzahl erreicht ein Motor bei seiner Nennspannung (z.B. 8,4 V) wenn er ohne mechanische Last (also ohne Luftschraube) betrieben wird. Dieser Wert ist eigentlich für alle Motoren angegeben. Bei Leerlaufdrehzahl zieht der Motor einen Leerlaufstrom "Ileer" aus dem Akku und verbrauch eine Leerlaufleistung Pleer. Damit kompensiert er nur die inneren Verluste.

unter Last
Belastet man den Motor mit einer Luftschraube, so muss er "mehr arbeiten" um zusätzlich zu sich selbst auch noch die Luftschraube zu drehen. Dadurch steigt der aufgenommene Strom und die Drehzahl sinkt. Je größer und steiler die Luftschraube ist, um so mehr Strom zieht der Motor und um so langsamer dreht er sich. Hält man den Motor schließlich fest, erreicht der Strom seinen Maximalwert: den Blockierstrom Imax. Da sich der Motor nun nicht mehr dreht, gibt er auch keine mechanische Leistung ab. Die abgegebene Leistung ist folglich im mittleren Drehzahlbereich am größten. In der Mitte seines Drehzahlbereichs ist auch die Stromaufnahme in der Mitte zwischen dem Leerlaufstrom und dem Blockierstrom. Da der Leerlaufstrom nur 1..3 A beträgt, hat ein Motor, der bei halber Leerlaufdrehzahl 27 A zieht, einen Blockierstrom von 54 A. Soll der Motor schon bei 2/3 seiner Leerlaufdrehzahl 30 A ziehen, ergibt sich ein Blockierstrom von 81 A.

Geeignet wäre in diesem Beispiel ein 8,4-V-Motor, der einen Blockierstrom von 60 ... 90 A aufweist. Leider geben nicht alle Motorhersteller den Blockierstrom ihrer Motoren an. Aber z.B. Graupner ist da auskunftsfreudig.

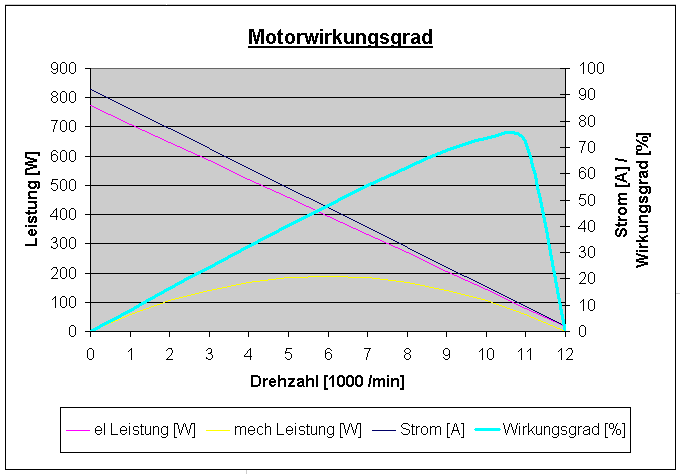
Folgende Grafik verdeutlicht die Zusammenhänge am Beispiel eines Motors mit einer Leerlaufdrehzahl von 12000/min  und einem Blockierstrom von 90A :

Die Grafik zeigt für unser Beispiel die elektrische Leistung Pelektrisch die der Motor vom Akku bekommt (rote Linie) und die mechanische Leistung Pmech, die der Motor über seine Achse an die Luftschraube abgibt (gelbe Linie) über den gesamten Drehzahlbereich (0 - 12000). Da die Akkuspannung immer gleich ist, erreicht man eine niedrige Drehzahl durch eine große Luftschraube und eine hohe Drehzahl durch eine kleine Luftschraube.

Mit steigender Drehzahl (kleinerer Luftschraube) sinkt zwar die vom Motor aufgenommene elektrische Leistung (rot), aber der Anteil der Leistung der dann auch in mechanische Leistung (gelb) umgewandelt wird steigt.

Der Wirkungsgrad des Motors (türkise Linie) steigt also mit der Drehzahl an, und erreicht bei knapp 11000 Umdrehungen/Minute sein Maximum.Bei einer kleinen hochtourenden Luftschraube sind also die Motorverluste am Kleinsten. Allerdings ist die Leistung des Motors bei diesen hohen Drehzahlen zu klein zum fliegen.

Man muss auch berücksichtigen, dass die Luftschraube bei der Wandlung der mechanischen Leistung in Vortrieb Verluste hat. Große (also langsamer drehende) Luftschrauben sind effektiver als kleine (hochtourige) Luftschrauben.

Der Kompromiss ist eine Drehzahl von etwa 2/3 der Leerlaufdrehzahl. In unserem Fall ergibt sich bei einer Drehzahl von 9000 Umdrehungen pro Minute ein Wirkungsgrad von ca 70%. Der Motor verbrät dabei 30% der elektrischen Leistung, das sind 225 W x 30% = 67,5 W. Dem Motordatenblatt ist zu entnehmen, ob der Motor das aushält, und ob er gekühlt werden muss (Luftstrom).

Falls die effektiven Drehzahlbereiche von Luftschraube und Motor nicht in Übereinstimmung zu bringen sind, muss ein Getriebe den hochtourigen Motor an die niedrigtourige Luftschraube anpassen. So ein Getriebe hat natürlich zusätzliche Verluste. In unserem Beispiel benutze ich den getriebelosen Direktantrieb.

---

Die Luftschraube

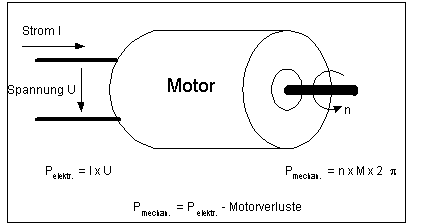
Hat man sich z.B. für einen 8,4 V-Motor mit 90-A Kurzschlussstrom entschieden, der eine Leerlaufdrehzahl von 12000/min aufweist, so liegt der gewünschte Arbeitspunkt des Motors bei 9000/min. Die Luftschraube sollte also für diese Drehzahl zugelassen sein.

mechanische Leistung
Bei 9000/min sollte die Luftschraube den Motor genau so sehr belasten, dass der Motor 30 A Strom aufnimmt. Von den 225 W elektrischer Leistung kommen an der Luftschraube noch ca 70% an, der Rest sind Verluste des Motors. Die Schraube bekommt also

Die mechanische Leistung Pmech ist das Produkt aus Drehzahl n und Drehmoment M.

Die Drehzahl ist schon festgelegt. Die Luftschraube muss bei 9000/min also ein Drehmoment von 160W / 9000/min = 160 W / (150Hz x 2 x 3,1415) =0,17 Nm aufweisen. Leider verraten die Hersteller uns die Drehmomente ihrer Luftschrauben nicht. Da ist ein anderer Weg zur idealen Luftschraube nötig.

Einer führt über die Homepage von W.Geck
Das Drehmoment ist proportional zum Quadrat der Drehzahl. Das heißt M = const x n x n, wobei const ein konstanter Wert einer bestimmten Luftschraube ist. Damit ist die mechanische Leistung proportional zur dritten Potenz der Drehzahl (hoch 3). Mit anderen Worten: für die doppelte Drehzahl braucht man die 8fache Leistung. Die doppelte Leistung ist schon für eine 1,26fachen Drehzahl nötig.
Herr Willhelm Geck hat für viele Luftschrauben die Drehzahl bei einer aufgenommene mechanischen Leistung von 100 W ermittelt (n100W) und auf seiner Homepage veröffentlicht. Da die Drehzahl proportional der Kubikwurzel der mechanischen Leistung ist, kann man aus diesem Wert die Drehzahl für jede Leistung oder die Leistung für jede Drehzahl bestimmen.
Das nötige n100W lässt sich wie folgt berechnen:

Beispiel:
n100W = n x 4,64 / Kubikwurzel (Pmechanisch) = 9000 x 4,64 / Kubikwurzel(160) = 9000 x 4,64 / 5,43 = 7690
Jede Luftschraube aus Gecks Tabellen mit einem n100W-Wert von ca. 7690 belastet unseren Motor also richtig, und sorgt für eine Drehzahl von 9000.
Nun hat jede Luftschraube aber eine Steigung und einen Durchmesser. Kleine Schrauben mit großer Steigung können die gleichen Drehmomente und n100W-Werte haben wie große Schrauben mit kleiner Steigung.

Das Drehmoment der Luftschraube hängt (neben der Drehzahl) von ihrem Durchmesser, ihrer Steigung und von ihrer aerodynamischen Qualität ab. Der Hersteller gibt den Durchmesser und die Steigung in Zoll (bzw. Zoll-pro-Umdrehung) an.

Steigung
Die Steigung der Luftschraube bestimmt zusammen mit der Drehzahl die maximale Fluggeschwindigkeit des Modells. Deshalb sollte man sich zunächst um die Steigung der Luftschraube Gedanken machen.
Soll das Modell z.B. 20 m/s (72 km/h) schnell fliegen, so muss die Luftschraube die Luft mit etwa der 1,5 .. 2 fachen Geschwindigkeit "nach hinten schrauben". Der Propellerluftstrom sollte also 30 m/s erreichen. Daraus und aus der Arbeitsdrehzahl unseres Antriebs kann man die nötige Steigung der Luftschraube in Zoll errechnen.

Für unser Beispiel ergibt sich
Steigung [Zoll] = 30 m/s x 2360 / 9000/min = 7,86 Zoll.

Als Luftschraube kommt also eine ??X8 in Frage. Diese Schraube ergibt bei 9000 Umdrehungen/Minute einen Luftstrahl mit einer Geschwindigkeit von 30,5 m/s.

Durchmesser
Damit steht die Steigung fest, und nun wählt man einen Durchmesser, der den Motor genau in gewünschtem Maße belastet. Dazu bräuchte man aber eigentlich Luftschraubendaten, die der Hersteller nicht nennt. Folgende empirisch ermittelte Formel hilft, versagt aber bei extremen Luftschraubenmaßen:

Für unser Beispiel ergibt sich also:
Durchmesser = Kubikwurzel(160) x 14500 / 9000 = 5,43 x 14500 / 9000 = 8,75 Zoll
Eine Luftschraube mit den Maßen 9x8 könnte also in etwa die gewünschten Eigenschaften haben. Je nach Hersteller kann aber auch eine 10x8 oder eine 11x8 die richtige Wahl sein.

In den Listen von Geck findet sich z.B. eine APC 9x8 mit einem n100W von 7260 /min. Die nehmen wir. Für diese Schraube ergibt sich bei 160 W mechanischer Leistung eine Drehzahl von 8490 /min. Die etwas verringerte Drehzahl führt ihrerseits aber zu etwas höheren mechanischen und elektrischen Leistungen (siehe Motordiagramm) und etwas schlechterem Motorwirkungsgrad. Aber so in etwa kommt das schon hin, insbesondere, da die etwas höhere mechanische Leistung wieder zu einer erhöhten Drehzahl führt. Irgendwo zwischen 8500 und 9000 Umdrehungen wird sich unser Antriebspaket einpendeln.

Schub
Der Schub der Luftschraube errechnet sich grob nach folgender Formel:

Das ist etwa 1 kg Schub, und das sollte für ein 1,5 kg schweres Modell mehr als ausreichen. Allerdings ist die Berechnung von Luftschrauben sehr ungenau. Ihr Wirkungsgrad und ihre aerodynamische Qualität sind in der Regel unbekannt. So kann der Schub auch vielleicht nur halb so groß sein.

---

Zusammenfassung

• Akku: 7-Zellen 1400 mAh
• Motor:  Leerlaufdrehzahl: 12000/min, Blockierstrom: 90 A
• Motorsteller: 30 A mit  BEC und  Bremse
• Luftschraube: 9x8, Klappluftschraube

• Maximalgeschwindigkeit: 20 m/s (72 km/h)
• Motorvollastlaufzeit: 3 Minuten